Probability
  1. Poker Probability Straight Flush Rules
  2. Poker Probability Straight Flush Video Poker
  3. Probability Of Straight Flush Poker
Poker probability straight flush valve

Poker Probability Straight Flush Rules

8921675656

1800 5726 991

  • Beginners Guide
  • How to Play
  • Leaderboards
    • Current Events
    • Past Events
  • Promotions
  • Support

Straight Flush Poker Hand Ranking

  1. Discover the numbers, strategy and odds behind the Straight Flush and the poker odds of flopping the top-best hand in poker.
  2. In the example of the four-flush, the player’s probability of filling the flush is approximately 36% after the flop (9 outs x 4) and 18% after the turn (9 outs x 2). Pot Odds Another important concept in calculating odds and probabilities is pot odds.

Straight Flush means any of the 5 cards in numerical order, all of identical suits. In the event of a tie, Highest rank at the top of the sequence wins the game. The best possible straight flush is known as a royal flush that consists of the ace, king, queen, jack and ten of a suit. There are two types of Straight. Straight flush. Any 5 cards of the same suit in sequence, such as 5♥, 6♥, 7♥, 8♥, 9♥. Ordinary straight. Five cards in sequence, with at least two cards of different suits. Ace can be high or low, but not both. Thus, A♠, 2♥, 3♦, 4♣, 5♥ and 10♠, J♥, Q♦, K♣, A♥ are valid straights; but Q♠, K♥, A♦, 2♣, 3♥ is not.

What is a Straight Flush?

Poker Probability Straight Flush

The next two tables show the probabilities in 5-card stud with one wild card. The first table is for a partially wild card that can only be used to complete a straight, flush, straight flush, or royal flush, otherwise it must be used as an ace (same usage as in pai gow poker). The second table is for a fully wild card.

Let's work out the analytical plan to find the probability of a straight flush

Poker Probability Straight Flush Video Poker

  • First, we have to count the number of five-card hands that can be dealt from a standard deck of 52 cards. This is a combination problem. The number of combinations is n! / r!(n - r)!. We have 52 cards in the deck so n = 52. And we want to arrange them in unordered groups of 5, so r = 5. Thus, the number of combinations is: 52C5 = 52! / 5!(52 - 5)! = 52! / 5!47! = 2,598,960 Hence, there are 2,598,960 distinct poker hands.
  • After that, we have to count the number of ways that five cards can be dealt to produce a straight flush. A straight flush consists of 5 cards in sequence, each card in the same suit. It requires two independent choices to produce a straight flush:
    • Choose the rank of the lowest card in the hand. For a straight, the lowest card can be an ace, 2, 3, 4, 5, 6, 7, 8, 9, or 10. So, we choose one rank from a set of 10 ranks. The number of ways to do this is 10C1.
    • Choose one suit for the hand. There are four suits, from which we choose one. The number of ways to do this is 4C1.
  • The number of ways to produce a straight flush (Numsf) is equal to the product of the number of ways to make each independent choice. Therefore, Numsf = 10C1 x 4C1 = 10 x 4 = 40

Conclusion: There are 40 different poker hands that fall in the category of straight flush.

  • Finally, we compute the probability. There are 2,598,960 unique poker hands. Of those, 40 are straight flushes. Therefore, the probability of being dealt a straight flush (Psf) is: Psf = 40 / 2,598,960 = 0.00001539077169

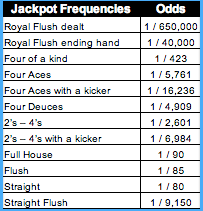
The probability of being dealt a straight flush is 0.00001539077169. On average, a straight flush is dealt one time in every 64,974 deals.

The Poker Hands Ranking are listed below,

  • Royal Flush
  • Straight Flush
  • Four of a Kind
  • Full House
  • Flush
  • Straight
  • Three of a Kind
  • Two Pair
  • Pair
  • High Card

Probability Of Straight Flush Poker

Copyright © Vollbet Network Pvt Ltd All Rights Reserved